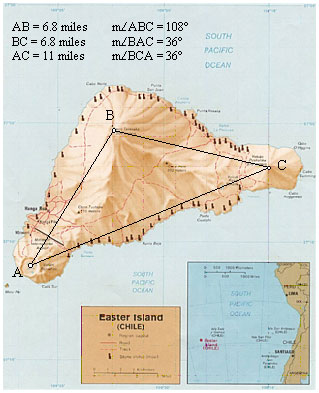
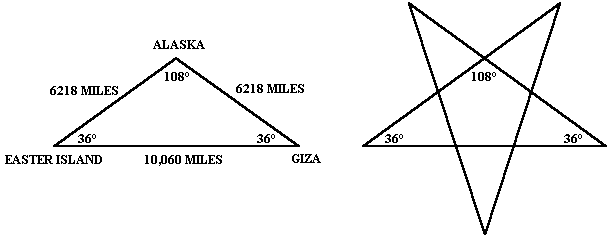
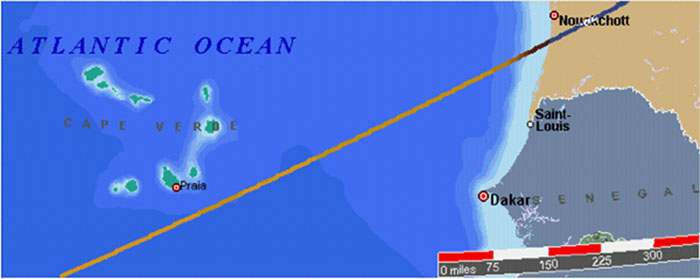
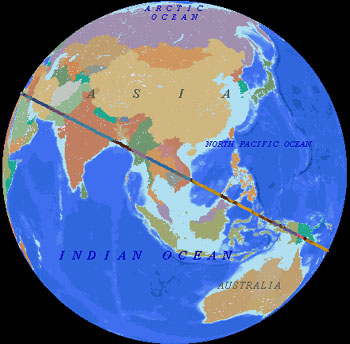
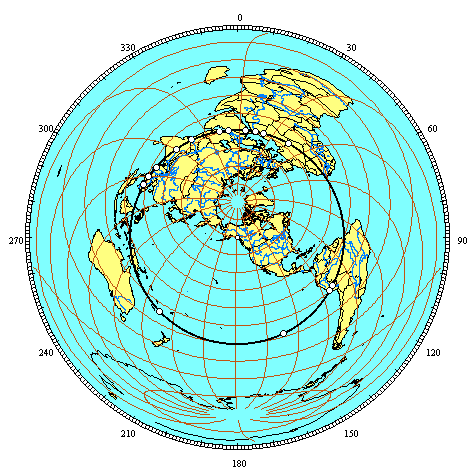
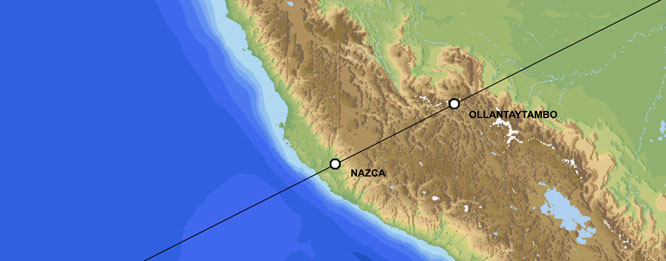
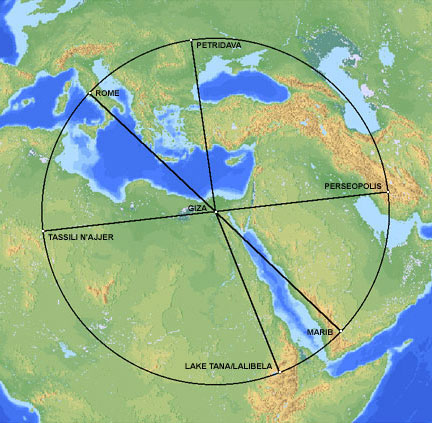
Great circles are straight lines that go all the way around the center of the earth. The equator is a great circle. Meridians of longitude that cross over the north and south poles are also great circles. For every location on a great circle, it's antipodal location is also on the circle. Other than the equator itself, any great circle crosses the equator at two antipodal locations, 180° apart. Other than the equator and meridians of longitude that run due north and south, any great circle reaches it's maximum latitudes at two locations that are 90° of longitude east and west of the two locations where the great circle crosses the equator.

Easter Island, Nazca, Ollantaytambo, Paratoari, Tassili n'Ajjer and Giza are all aligned on a single great circle. Additional ancient sites that are located within one tenth of one degree of this great circle include Petra; Perseopolis; Khajuraho; Pyay, Sukothai and Anatom Island.

Near Ollantaytambo, Machupicchu and Cuzco are within one quarter of a degree. The Oracle at Siwa in the western Egyptian desert is within one quarter of a degree. In the Indus Valley, Mohenjo Daro and Ganweriwala are within one quarter of a degree. The ancient Sumerian city of Ur and Angkor temples in Cambodia and Thailand are within one degree of the great circle. The Angkor temple at Preah Vihear is within one quarter of a degree.

This circle crosses over the source and the mouth of the Amazon, the dividing line between upper and lower Egypt, the mouth of the Tigris-Euphrates, the Indus River and the Bay of Bengal near the mouth of the Ganges. The circle also crosses over a number of areas of the world that are largely unexplored, including the Sahara Desert, the Brazilian Rainforest, the highlands of New Guinea, and underwater areas of the North Atlantic Ocean, the South Pacific Ocean and the South China Sea.

The alignment of these sites is easily observable on a globe of the earth with a horizon ring. Aligning any two of these sites on the horizon ring will align all of these sites on the ring. 3-D world atlas software programs will also draw this great circle around the earth. The four images below are centered on the two locations where the great circle crosses the equator and the two locations where the great circle reaches it's maximum latitudes. The circle crosses over the equator at 48° 36' west longitude and 131° 24' east longitude. The maximum latitude of the circle is 30° 22' north latitude at 41° 24' east longitude and 30° 22' south latitude at 138° 36' west longitude.

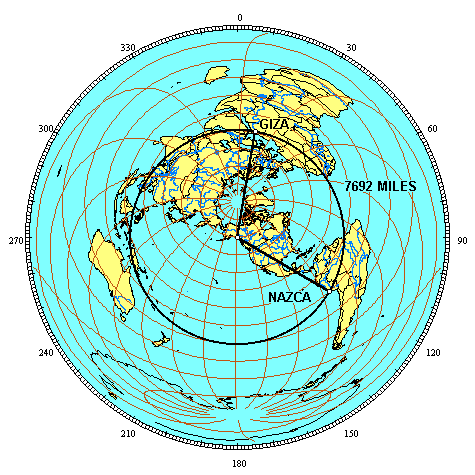
JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

All great circles have two antipodal axis points. The two axis points for the equator are the north and south poles. Every point along the equator is equally distant at 90°, or one quarter of the circumference of the earth, from the north and south poles. For any great circle, the distance from the axis points to any point along the circle is one quarter of the circumference of the earth. For any great circle other than the equator, the longitude of the axis points are 90° east and west of the two points where the great circle crosses the equator.

Great circles that run due north-south along meridians of longitude have their axis points on the equator, 90° of longitude east and west of the points where the meridian circle crosses the equator and 90° of latitude from the poles where meridian circles reach their maximum latitudes. The distance from the axis points to any point along a meridian circle is one quarter of the circumference of the earth, but 90° of longitude from the axis point to the point where the meridian circle crosses the equator is 6,225 miles, while 90° of latitude from the axis point to the maximum latitude of the meridian circle at the poles is 6,215 miles. This is because the polar circumference of the earth is 24,860 miles, while the equatorial circumference is 24,901 miles, due to the bulge of the earth at the equator and the flattening of the earth at the poles.

Our modern system of calculating degrees of latitude from the equator to the poles is based on the north-south angular change along the surface of the earth. As a result, degrees of latitude are slightly longer at the poles, where the earth is flatter, and slightly shorter at the bulge of the equator. For great circles other than the equator and other than meridian circles, the north-south distance from the axis points to the great circle crosses over the pole in one direction, while it crosses over the equator in the other direction. As a result, the latitude of the axis points must be adjusted slightly to compensate for the longer distance of degrees of latitude at the poles and the shorter distance of degrees of latitude at the equator.

The two axis points for the great circle illustrated above are located at 59° 53' north latitude and 138° 36' west longitude and at 59° 53' south latitude and 41° 24' east longitude. The southern axis point is in deep water approximately 500 miles from the coast of Antarctica. The northern axis point is in the northwestern corner of Canadian British Columbia on a glaciated ridge line approximately 6,500 feet above sea level. The circumference of this great circle is 24,892 miles. This is slightly less than the equatorial circumference of the earth, but closer to the equatorial than the polar circumference because the maximum latitude of the great circle is closer to the equator than the poles, and because most of the shortening of the polar circumference is due to the flattening of the earth near the poles.

The chart below lists the distance of each site from the great circle and the distance of each site from the northern axis point. There are slight variations in the distance from the axis point to the great circle depending on whether the route from the axis point to different locations along the great circle crosses over the equator or polar regions. The mean distance from the axis point to the great circle is 6,218 miles.

	Latitude	Longitude	To Great Circle:	To Axis Point:
Giza	29° 59' N	31° 09' E	0 miles	6.219 miles
Siwa	29° 14' N	25° 31' E	10 miles	6,231 miles
Tassili n'Ajjer	26° 32' N	9° 50' E	0 miles	6,218 miles
Paratoari	12° 48' S	71° 25' W	0 miles	6,219 miles
Ollantaytambo	13° 15' S	72° 16' W	0 miles	6,220 miles
Machupicchu	13° 06' S	72° 35' W	15 miles	6,206 miles
Nazca	14° 42' S	75° 06' W	0 miles	6,221 miles
Easter Island	27° 06' S	109° 20' W	0 miles	6,221 miles
Aneityum Island	20° 10' S	169° 48' E	8 miles	6,230 miles
Preah Vihear	14° 24' N	104° 40' E	25 miles	6,241 miles
Sukhothai	17° 01' N	99° 42' E	5 miles	6,226 miles
Pyay	19° 15' N	95° 05' E	5 miles	6,213 miles
Khajuraho	24° 51' N	79° 56' E	12 miles	6,206 miles
Mohenjo Daro	27° 15' N	68° 17' E	20 miles	6,243 miles
Persepolis	29° 56' N	52° 55' E	5 miles	6,215 miles
Ur	30° 57' N	46° 07' E	40 miles	6,173 miles
Petra	30° 19' N	35° 28' E	6 miles	6,213 miles

The sites listed above are shown clockwise from Giza on the equal azimuthal projection below. The projection is centered on the axis point in southeastern Alaska. Distances to any location from the center of an equal azimuthal projection are equally scaled. Since all of the sites on the great circle alignment are equally distant from the axis point at one quarter of the circumference of the earth, the alignment forms a perfect circle halfway between the center and the outer edge of the projection.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

BACK

THE GOLDEN SECTION

PART II

The Greek letter phi (φ) signifies the golden section, also known as the divine proportion of 1.618 to one. The mathematical formula for φ is the square root of five plus one, divided by two. If a line is divided with the ratio of φ between the longer segment and the shorter segment, the ratio between the whole line and the longer segment is also φ. Given a length of one for the shorter segment, the length of the longer segment is φ and the length of the entire segment is φ plus one. φ plus one is also equal to φ²:

1.618 + 1 = 2.618 and
1.618 x 1.618 = 2.618

Given a length of one for the longer segment, the shorter segment is 1/φ (.618) and the length of the entire segment is φ. 1/φ is also equal to φ minus one:

1 ÷ 1.618 = .618 and
1.618 minus 1 = .618

There is also an extremely close mathematical relationship between φ and π expressed as φ² x 6 = π x 5 (2.618 times 6, divided by 5, equals 3.1416). There is an ongoing dispute about whether or not there was an ancient awareness of φ and π. In the ancient world, φ existed naturally in the proportions and growth rates of plant and animal species, as well as spirals ranging from microscopic to flowering plants and seashells to the spiral arms of the galaxy. The π ratio between the diameter and the circumference of a circle also existed naturally in the ancient world. It has also been shown that φ and π existed in many man-made ancient buildings, including the great pyramid of Giza.

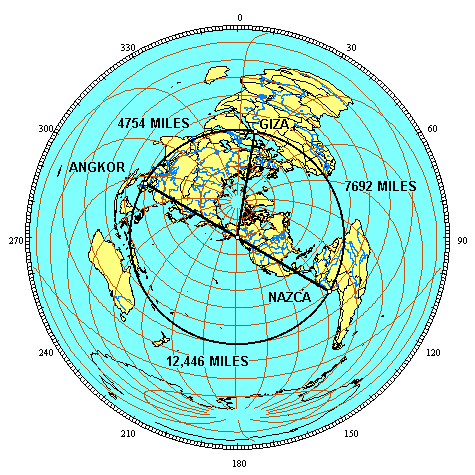
JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The ancient Egyptian royal cubit, equal to 20.625 English inches, was used to build the great pyramid. The height of the pyramid is 280 cubits and the baselength of the sides at ground level is 440 cubits. The ratio between the height and two baselengths of the pyramid is an accurate expression of π (880/280 = 3.1428). The slant height of the pyramid is 356 cubits. The ratio between the baselength of the pyramid and the two slant heights that form the pyramid triangle is an accurate expression of φ (712/440 = 1.618).

Angkor Wat is 4,745 miles from the Great Pyramid and the Great Pyramid is 7,677 miles from Nazca. This is a precise expression of φ:

4,745 x 1.618 = 7,677

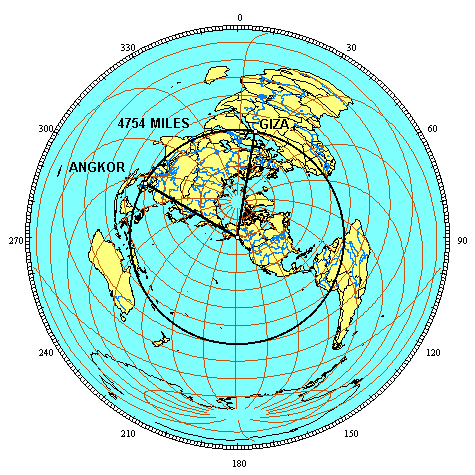
Ninety miles northeast of Angkor Wat are the Angkor temples at Prassat Preah Vihear. Preah Vihear is 4754 miles from the Great Pyramid. The line of ancient sites crosses over the Great Pyramid and Angkor Vihear.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS Twenty five miles northwest of the city of Nazca is a figure known as the Hummingbird. The Hummingbird is 7,692 miles from the Great Pyramid. The line of ancient sites also crosses over the Hummingbird.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

The relationship between the distances from Angkor Vihear to the Great Pyramid and from the Great Pyramid to the Nazcan Hummingbird is also a precise expression of φ:

4,754 x 1.618 = 7,692

Because the Hummingbird and Angkor Vihear are antipodal sites, with a distance between them of one-half of the circumference of the earth, two Golden Section relationships between these three sites are shown by the circumference of the earth along the line of ancient sites:

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

4,754 x 1.618 = 7,692 4,754 + 7,692 = 12,446, and 7,692 x 1.618 = 12,446

These Golden Section relationships may also be diagramed on a straight line:

The line of ancient sites is a line, from the perspective of the first illustration in Part One, and it is a circle, from the perspective of the azimuthal projection above. The line and the circle are found in the greek letter φ and the number 10. Zero and one are also the first two numbers and the only two numbers in the binary code.

The φ relationships between these sites are reflected repeatedly in the first 500 Fibonacci numbers. The first three prime numbers, 2, 3 and 5, approximate the intervals along the circumference of 20%, 30% and 50%, between these three sites. This same percentage of the circumference relationship, accurate to three digits, is found in Fibonacci numbers 137-139:

Percentage of circumference:        First three digits of Fibonacci numbers:
Angkor to Giza: 19.1%                                                                         #137: 191... (Prime)
Giza to Nazca: 30.9%    #138: 309...
Nazca to Angkor: 50.0%                                                                     #139: 500...

The next prime Fibonacci number after #137 is #359. The distances between these sites, in miles, is reflected by Fibocacci numbers 359-361, accurately to five digits:

Distance between sites: First five digits of Fibonacci numbers:
Angkor to Giza: 4,754 miles #359: 47542... (Prime)
Giza to Nazca: 7,692 miles #360: 76924...
Nazca to Angkor: 12,446 miles #361: 12446...

BACK

NAZCA

PART III

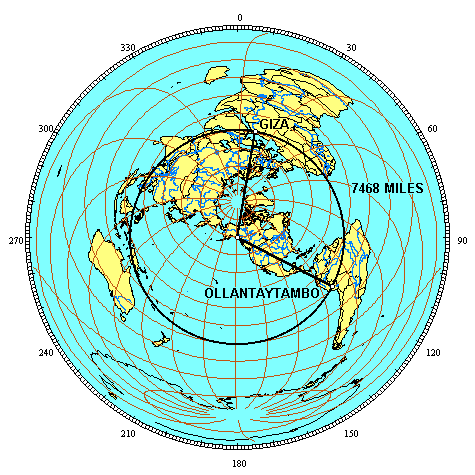
JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The glyphs and lines at Nazca are oriented along the alignment of ancient sites. The image below of the glyphs at Nazca with a compass bearing, is available on the internet, but it is usually oriented away from the cardinal points so that the figures are roughly horizontal and vertical. Rotating this image so that the north-south axis is vertical, aligns most of the figures and geometric drawings with the alignment of ancient sites as it crosses Nazca.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The illustration of the Nazca lines above has also been rotated so that the north-south axis is vertical, and shows the primary orientation of the lines is from southwest to northeast, matching the great circle alignment of ancient sites as it crosses Nazca.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The distance from the Nazca lines to Giza is 7692 miles. The distance from the axis point in southeastern Alaska to Giza and to Nazca is 6218 miles, forming an isosceles terrestrial triangle with a baselength of 7692 miles and sidelengths of 6218 miles.

The 3D global image above is centered in the middle of the terrestrial triangle. As a result, all three of the great circle segments are curved. The equal azimuthal projection below is centered on the axis point. As a result, the great circle segments from the axis point to Giza and to Nazca are straight lines. 7692 miles is 30.9% of the circumference of the great circle (7692/24,892 = .309) or 111.245° along the great circle (.309 x 360 = 111.245 ). The azimuth of the great circle segment from the axis point to Giza is 9° and the azimuth of the great circle segment from the axis point to Nazca is 120°, showing that the angle at the axis point is also 111°. The distance from the axis point to Giza and to Nazca is one quarter of the circumference of the earth, or 90°. Since the great circle segments from the axis point are perpendicular to the great circle itself, the angles at Giza and Nazca are also 90°.

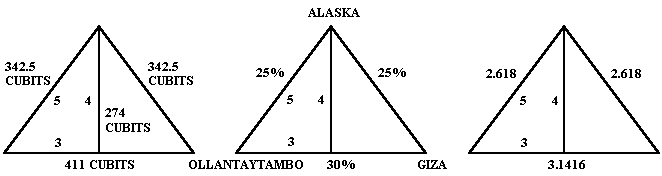
JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

A simple spherical trigonometry formula converts the 90° - 90° - 111° spherical triangle to an equivalent flat surface triangle. The angle opposite the baselength is divided by two (111.235°/2 = 55.6225°), and then divided by the angle adjacent to the baselength (55.6225°/90° = .618). The φ reciprocal is .618 (1/φ). Applying the inverted cosine function to .618 gives 51.83° for the flat surface equivalents of the 90° spherical angles at Nazca and Giza. These are the same as the angular dimensions of the great pyramid. Alternatively, the two great circle segments from the axis point to Nazca and from the axis point to Giza are each 25% of the circumference of the earth while the great circle segment from Nazca to Giza is 30.9% of the circumference of the earth. The two great circle segments from the axis point to Nazca and to Giza add up to 50% of the circumference of the earth and 50/30.9 = 1.618, also demonstrating that these three great circle segments form a triangle equivalent to the crossection of the great pyramid, with the same φ proportion:

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS This relationship may also be shown using the distance between the three points in miles. One quarter of the circumference of the earth (along the great circle alignment) is 6223 miles (24,892/4 = 6223). The two sides of the terrestrial triangle are 6223 miles long, for a combined length of 12,446 miles. The distance from Giza to Nazca is 7692 miles and 12,446/7692 = 1.618. The above calculation is based on a round earth assumption. Although the great circle segments from the axis point to the great circle are 90° or one quarter of the circumference of the great circles from the axis points, the circumference of the great circles that cross over the axis point are actually a bit shorter than the circumference of the main great circle because the axis point is closer to the pole than the primary great circle that crosses over Giza and Nazca. The mean distance from the axis point to the great circle is 6218 miles, five miles less than one quarter of the circumference of the primary great circle, just as the distance from the north and south poles to the equator is 6215 miles even though one quarter of the equatorial circumference of the earth is 6225 miles (24,901/4 = 6225).

Given side lengths of 6218 miles from the axis point to Giza and Nazca, the distance from Giza to Nazca would have to be 7686 miles for the φ ratio to be exact, based on an ellipsoidal earth model. The main group of lines and figures at Nazca that is included as a UNESCO world heritage site is approximately 25 miles E-W and 4 miles N-S. The distance of 7692 miles from Giza along the great circle and the distance of 7686 miles from Giza along the great circle both fall within the main part of the Nazca lines and figures that are designated by UNESCO for protection as a world heritage site, so in the case of Nazca the φ relationship is present with either a round earth assumption or an ellipsoidal model.

BACK

OLLANTAYTAMBO

PART IV

Ollantaytambo is 7468 miles from Giza. 30% of the circumference of the great circle is 7468 miles (24,892 x .3 = 7468). Ollantaytambo is precisely 30%, or 108° along the great circle, from Giza. The azimuth from the axis point to Giza is 9° and the azimuth from the axis point to Ollantaytambo is 117°, also showing that the terrestrial angle at the axis point is 108°. The angles at Ollantaytambo and at Giza are 90° and the distance from the axis point to Ollantaytambo and to Giza is 90° or 25% of the circumference of the earth.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The height of the second pyramid at Giza is 274 cubits and the baselength of the sides at ground level is 411 cubits. The ratio between the height and the baselength is 2/3. The slant height of the pyramid is 342.5 cubits. The triangle formed by the half-base, the height and the slant height is a perfect 3-4-5 right triangle. The ratio between the baselength and the slant height is 6/5. These are the same dimensions as the terrestrial triangle from the axis point to Ollantaytambo and Giza with a baselength of 30% and side lengths of 25%.

φ² x 6/5 = π (2.618 x 6/5 = 3.1416). This terrestrial triangle (and the second pyramid at Giza) have a ratio between the baselength and the sidelength of 3.1416 : 2.618.

BACK

ANGKOR

PART V

Angkor Preah Vihear is 4754 miles from Giza. This is 19.1% of the great circle circumference, or 68.754° (19.1% times π equals 60.00% and 68.754° times π equals 216.00°). The two great circle segments from the axis point to Giza and to Angkor Vihear are each 90°, or 180° combined. 180°/68.754° = 2.618. The ratio between both sides of this terrestrial triangle and the baselength of the triangle is 2.618 to one.

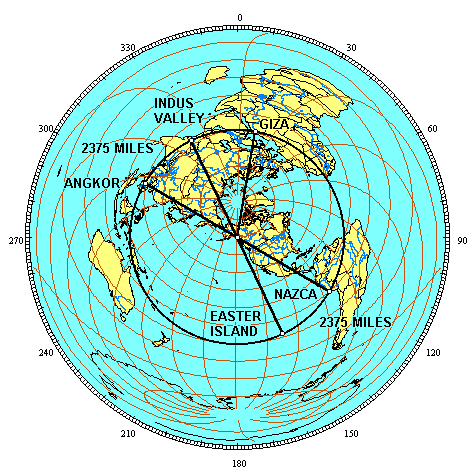
JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

The image below is centered on Angkor Wat and the circle is 1,466.6 miles away. East of Xian, the Longmen caves are close to this alignment. Just south of Dieng, Borobudur and Prambanan are also close to this alignment.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

Links	Latitude	Longitude	Distance to Angkor Wat
Xian	34°15' N	108°55' E	1,474 miles
Yonaguni	24°26' N	123°00' E	1,464 miles
Bada Valley	1°00' S	119°50' E	1,483 miles
Dieng	7°12' S	109°54' E	1,489 miles
Bodh Gaya	24°42' N	84°58' E	1,461 miles
Mt. Everest	27°58' N	86°56' E	1,484 miles

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The image below is centered on Giza and the circle is 1,320 miles away. Lake Tana, the source of the Blue Nile, is west of Lalibela and right on this alignment. Also in the highlands of Ethiopia, north of Lalibela, is the sacred city of Axum. The radius of the Giza alignment is 9/10ths of the Angkor alignment: 1320/1466.6 = 0.9

Links	Latitude	Longitude	Distance to Giza
Rome	41° 53' N	12° 30' E	1,326 miles
Petridava	48° 48' N	26° 35' E	1,326 miles
Persepolis	29° 56' N	52° 55' E	1,304 miles
Marib	15° 26' N	45° 20' E	1,350 miles
Lalibela	12° 02' N	38° 50' E	1,337 miles
Tassili n'Ajjer	26° 32' N	9° 50' E	1,320 miles

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS Giza is 4,745 miles from Angkor Wat. The midway point along the great circle path from Giza to Angkor Wat is at approximately 26° 15' N 70° 00' E, in the Indus Valley. This is approximately 100 miles east of Mohenjo Daro, closer to the unexcavated Indus Valley city of Ganweriwali. This location is also within one degree of being exactly antipodal to Easter Island. The circle is 2,372.5 miles away from the midpoint in the Indus Valley. As this alignment follows the course of the Nile in Egypt, it comes close to several ancient Egyptian sites in addition to Giza, including Abydos and Amarna. In Turkey, Catal Hoyuk is just inside this alignment.

In addition to crossing over the center of the alignments around Angkor and around Giza, the Indus Valley alignment also crosses over the perimeter of the other two alignments at significant locations (Lake Tana and Xian). The radius of the Angkor alignment times 1.618 equals the radius of the Indus Valley alignment and the radius of the Indus Valley alignment times .618 equals the radius of the Angkor alignment, demonstrating the φ relationship between the two alignments:

1,466.6 miles x 1.618 = 2,372.5 miles 2,372.5 miles x .618 = 1,466.6 miles

	Latitude	Longitude	Distance to: 26° 15' N 70° 00' E
Giza	29° 59' N	31° 09' E	2,372 miles
Angkor Wat	13° 28' N	103° 53' E	2,366 miles
Lake Tana	11° 50' N	37° 00' E	2,365 miles
Xian	34° 15' N	108° 55' E	2,376 miles

BACK

EASTER ISLAND

PART VI

Easter Island is triangular and the three volcanic peaks on Easter form an isosceles triangle with an apex angle of 108° and base angles of 36°. The ratio between the length of the base and the lengths of the sides is φ (6.8 miles x 1.618 = 11 miles).

The southern coastline is roughly parallel to the great circle as it crosses over the island. The southwestern corner of Easter is 10,060 miles from Giza. The length of the great circle segments from the axis point to Easter and to Giza is 6,218 miles.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The ratio between the baselength of 10,060 miles and the side lengths of 6,218 miles is φ (6,218 x 1.618 = 10,060). The azimuth from the axis point to Giza is 9° and the azimuth from the axis point to Easter is 154°. The angle of the terrestrial triangle at the axis point is 145°. The terrestrial angles at Easter and Giza are 90°. These terrestrial angles convert to flat surface angles of 108° at the axis point and 36° at Easter and Giza. This is the same triangle that is formed by the three volcanic peaks on Easter and the same triangle that is found in a pentagram.

The φ ratio between the distance from Easter to Giza and the distances from the axis point to Easter and Giza is also shown by these measures in kilometers. One quarter of the circumference of the earth is 10,000 kilometers. The distance from Easter to Giza is 16,180 kilometers, expressing the φ ratio of 1.618 : 1.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS Easter is 2375 miles from Nazca. This is 9.54% of the circumference of the earth, or 34.34°. The axis point is 6218 miles from Easter and from Nazca. The ratio between one side of the terrestrial triangle and the baselength of the triangle is 2.618 to one (2375 miles x 2.618 = 6218 miles). The terrestrial triangle formed by Angkor Vihear, Easter’s antipodal point in the Indus Valley and the axis point has these same dimensions with the same φ² ratio between the side length and the base length. The terrestrial triangle formed by Easter’s antipodal point in the Indus Valley, Giza and the axis point has these same dimensions and the same φ² ratio.

BACK

LINES THROUGH THE EARTH

PART VII

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The alignment of ancient sites may be viewed as a circle because all of the sites are on a straight line around the center of the earth. The two points where the circle crossse the equator are on the horizontal axis, and the two points where the circle reaches the highest latitudes are on the vertical axis. The center of the circle is the center of the earth. The distance from the center of the earth to any point on the circle is the radius of the earth (24,892 ÷ π ÷ 2 = 3962 miles).

The great circle distance from Easter Island to Nazca is 2375 miles, or 9.54% of the great circle (2375/24,892 = 09.54) or 34.344° (.0954 x 360 = 34.344°). This also gives 34.344° for the angle between the two sites at the center of the earth. One half of this angle is 17.172°.The straight line distance between the two sites is equal to the sine of one half of their angle at the center of the earth times the diameter of the earth. The sine of 17.172° is .29524. The diameter of the earth (7924 miles) times .29524 gives 2339.5 miles for the straight line (through the earth) distance from Easter to Nazca. The height of a triangle with sides of 3962 miles and a baselength of 2339.5 miles is 3785 miles. The baselength of the triangle times φ is equal to the height of the triangle (2339.5 x 1.618 = 3785). The center of the earth, Angkor and Easter’s antipodal point in the Indus Valley forms this same φ triangle, as does the triangle formed by the center of the earth, the Indus Valley and Giza.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The length of the base of each face of the Great Pyramid is 440 cubits. The slant height of each face is 356 cubits. One half of the length of the base times φ equals the slant height of the Great Pyramid:

440 cubits ÷ 2 = 220 cubits

220 cubits x 1.618 = 356 cubits

The ratio of the base to the slant height of the Great Pyramid is exactly two times the ratio of the base to the height of the throught the earth triangles shown above.

Just south of Giza, the step pyramid at Saqqara is believed to have been the first stone pyramid built in Egypt.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The steps of this pyramid have been estimated to be inclined to the vertical in the range of 16°-18°. Recent measurements by Jon Bodsworth indicate a 17° angle of inclination. Measurements by Robert Bauval also indicate an angle of 17° with a margin of error of plus or minus 20'. An inclination of 17.172° (17° 10') to the vertical gives an inclination of 72.828° to the horizonal, the same as the through earth terrestrial triangles shown above:

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The 2φ ratio between the base and the height of the right triangle formed by the inclination of the pyramid steps is the same as the 2φ ratio between the half-base and the height of the through earth terrestrial triangles shown above.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS 10 miles southwest of Easter Island is a point along the great circle alignment that is equally distant at 10,071 miles from Giza and Angkor Vihear. Through earth lines from this point to Angkor and Giza are 7571 miles long. A great circle distance from Giza to Angkor of 4750 miles converts to a straight line distance of 4470.5 miles. The height of this straight line triangle is 7233.5 miles. The base angles of the triangle at Giza and Angkor are 72.828° and the φ ratio between the height and the base of the triangle is the same as the through earth triangles shown above: 4470.5 x 1.618 = 7233.5

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The straight line distance from Easter Island to Machupiccu is 2522 miles (great circle distance: 2566 miles). The straight line distance from Easter to it's antipodal point in the Indus Valley is 7924 miles (diameter of the great circle). The straight line distance from Easter to Giza is 7566 miles and the straigth line distance from Easter to Angkor Wat is 7574 miles.

The straight line distance, through the Earth, from Angkor Wat to Easter (7,574 miles), plus the straight line distance from Easter to Macchupicchu (2,522 miles), equals the great circle distance from Angkor Wat to Easter (10,096 miles).

The straight line distance from the Great Pyramid to Easter (7,566 miles) is three times the straight line distance from Easter to Machupicchu (2,522 miles).

The straight line distance from Easter to its antipodal point in the Indus Valley (7,924 miles), which is also the diameter of the Earth, is 3.1416 times the straight line distance from Easter to Machupicchu (2,522 miles), a precise expression of π.

Since the circumference of the Earth is also 3.1416 times the diameter of the Earth, the straight line distance from Easter to Machupicchu times π² equals the circumference of the Earth.

BACK

SINE WAVES

PART VIII

As the Earth rotates on it’s axis, the Equator remains aligned, but the line of ancient sites describes a sine wave as a result of it’s tilt relative to the Equator. The line of the ecliptic may be observed describing a similar wave by spinning a globe that has a line of the ecliptic. The wave may also be visualized by drawing the line of ancient sites on a flat projection of the Earth.

The wavelength is equal to the circumference of the Earth. The amplitude of this wave, measured from the middle of the wave (the equator), is 30° of latitude. Recall that the 30th parallels are ½ of the height of each hemisphere, or ½ of the radius of the Earth.

Since the height of the wave is equal to ½ of the Earth’s radius, the ratio between the wavelength and it’s amplitude is 4π. Measuring the amplitude from the top of the wavelength to the bottom (from 30° N to 30° S), the amplitude is equal to the radius of the Earth, and the ratio between the wavelength and the amplitude is 2π.

BACK

IN SEARCH OF ATLANTIS

PART IX

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The story of Atlantis is generally credited to Plato, even though he ascribed the story to much earlier Egyptian sources. According to those sources, the ancient, advanced Atlanteans ruled over islands and continents from an island kingdom outside of the Pillars of Hercules, which is thought to be the Straights of Gibralter. In Greek mythology, Atlas was the first king of Atlantis. Atlas had seven daughters known as the Atlantides. Because their mother was named Hesperis, they were also known as the Hesperides.

Machupicchu and the Great Pyramid are equally distant from the Cape Verde Islands. Easter Island and the Indus Valley are also equally distant from Cape Verde. When the Cape Verde Islands were rediscovered by European mariners in 1460 they were found to be uninhabited. However, islands in this location are found on earlier maps and described as inhabited in ancient times.

The Mecia de Viladestes map of 1413 shows islands in the location of Cape Verde labeled Gades. The information in this map is thought to have come from Roman sources dating back to the first century AD.

The discoveries of the world from their first originall unto the yeere of our Lord 1555, written by Antonio Galvao in 1563, lists the ancient names for the Cape Verde Islands as the Dorcades, Hesperides and the Gorgades. A 1587 map by Richard Hakluyt also labels the Cape Verde Islands as the Gorgades and the Hesperides.

According to Plato, there was a mountainous region north of the city of Atlantis. One possible location for Atlantis is in the Atlantic Ocean, just south of the Cape Verde Islands.

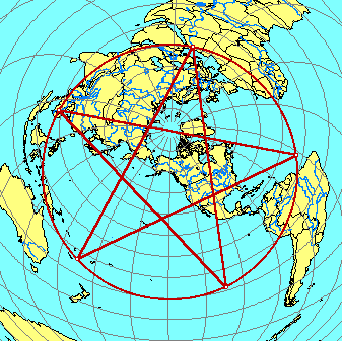
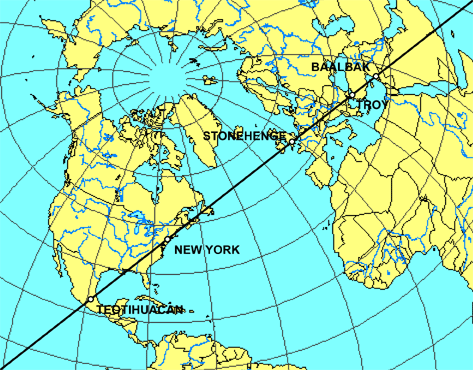
JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS Arysio Nunes dos Santos proposed that Atlantis was originally located in the Bay of Bengal, just south of the mouth of the Ganges, and in the South China Sea. These areas were above sea level during the earth's last glaciation. The landmass that forms the shallow bottom of the South China Sea is the only known area on earth, large enough to meet Plato's description of the size of Atlantis, that sank at the end of the last ice age. Santos argues that scientific evidence, and references in ancient writings, folklore and myths, prove that the South China Sea and the Bay of Bengal were the original sites of Atlantis and Lemuria. Santos contends that a super eruption of Krakatoa in Atlantean times destroyed Atlantis and caused the end of the last ice age by covering the earth with volcanic ash which absorbed sunlight and melted the ice. The alignment of world wonders crosses over the Bay of Bengal, just south of the mouth of the Ganges, and goes right across the middle of the South China Sea. The halfway point betwen Mohenjo-Daro and Angkor is also located in the Bay of Bengal.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS Another possible Atlantis location is halfway between the Great Pyramid and Easter Island, at 4° 19' north latitude, 41° 30' west longitude, under the Atlantic Ocean northeast of the mouth of the Amazon. On the diagram below, the marked locations are Giza, Angkor, Anatom Island, Easter Island, and 4° 19' north latitude, 41° 30' west longitude in the Atlantic Ocean. The distance from the Great Pyramid to Easter Island is approximately 40% of the circumference of the earth. The marked location in the Atlantic is halfway between the two, 20% each way. Machupicchu is halfway between Easter Island and the marked location in the Atlantic, 10% each way. The Distance from the Great Pyramid to Angkor Wat is approximately 20% of the circumference, and the Indus Valley is halfway between the two, 10% each way. The Distance from Easter Island to Angkor Wat is approximately 40% of the circumference, and Anatom Island is halfway between them, 20% each way. Although there are no islands in the Atlantic near 4° 19' north latitude, 41° 30' west longitude, it is interesting to note that the famous Piri Reis map shows a large island in this location, and the geology of recent core samples, taken from the ocean floor in this area, is of continental rather than oceanic type rock.

BACK

OTHER GREAT CIRCLE ALIGNMENTS OF ANCIENT SITES

PART X

• A SECOND EASTER ISLAND ALIGNMENT also includes Tiahuanaco, Bandiagara Dendera, Luxor, Mohenjo-Daro, Varanasi, Bodh Gaya and Mandalay.

• A THIRD EASTER ISLAND ALIGNMENT also includes Fatima, Filitosa, Rome, Constantinople, Hattusas, Van, Mehrgarh, Mohenjo-Daro and Bali.

• A FOURTH EASTER ISLAND ALIGNMENT also includes Napata, Mecca, Mohenjo-Daro, Mohenjo-Daro, Agra, Kathmandu, Pohnpei and Tahiti.

• A SECOND GREAT PYRAMID ALIGNMENT also includes Jerusalem, Xian, and Pohnpei.

• A THIRD GREAT PYRAMID ALIGNMENT also includes La Quemada, Poverty Point, Serpent Mound, Brittany, Rome, Alexandria, Mecca and Marib.

• A SECOND PERSEOPOLIS ALIGNMENT also includes Nippur, Baalbek, Byblos, Palaikastro, Knossos, Malta, Timg alt="JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS"ad, Volubilis and Ingapirca.

• A SECOND ANGKOR ALIGNMENT also includes Paracus, Newgrange, Castlerigg, Gotland, Zagorsk, Llasha, Phimai and Uluru.

• A SECOND NAZCA ALIGNMENT also includes Tiahuanaco, Khami, Great Zimbabwe, Angkor Wat, Preah Vihear, My Son and Hawaii.

• A SECOND MACHUPICCHU ALIGNMENT also includes Ollantaytambo, Saqsaywaman, Cusco, Ingapirca, Tazumal, Mixco Viejo, Bonampak, Palenque, La Venta, Mesa Verde and Chaco Canyon.

• A SECOND CHACO CANYON ALIGNMENT also includes Cahokia Mounds, the Newark Earthworks, Audaghast, Koumbi Saleh Djenne, and Meteor Crater, Arizona.

• A SECOND PALENQUE ALIGNMENT also includes Coba, Bimini, Fatima, Abydos, the Valley of the Kings, Luxor, Mecca and Taupo.

• CONVERGENT ALIGNMENTS include Easter Island, Chaco Canyon, Palenque, Ingapirca, Nazca, Ollantaytambo, Bandiagara, Fatima, Rome, Siwa, Giza, Luxor, Mecca, Perseopolis, Mohenjo-Daro, Angkor and Pohnpei.

BACK

THE NEW ATLANTIS

PART XI

The old urban centers on the Eastern Seaboard of the U.S are in nearly perfect alignment. The image below is a cropped 3D projection centered on New York City.

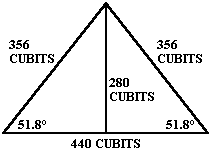
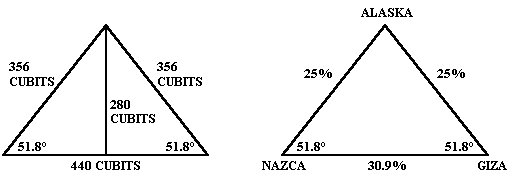
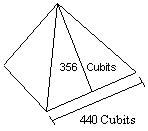JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS

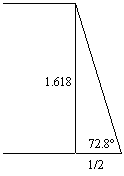
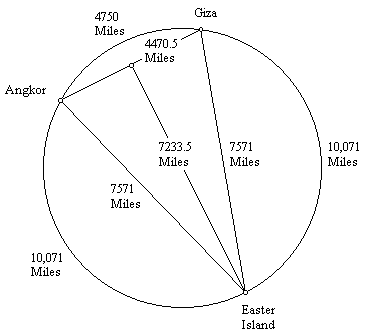
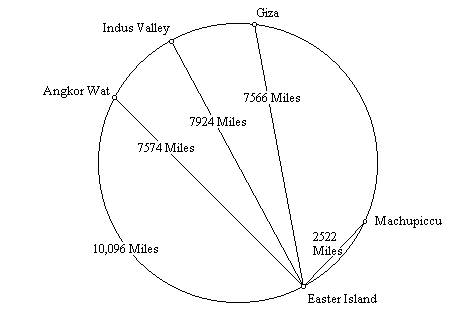
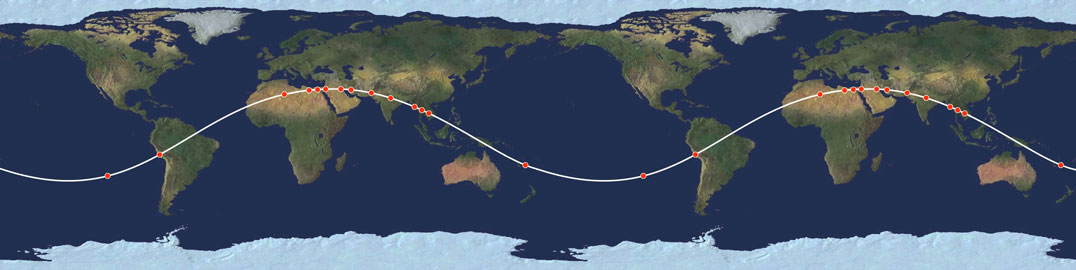JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS This great circle line crosses through the middle of Washington DC and the middle of Boston, and it crosses right over the middle of New York City. It also crosses over Philadelphia and the Baltimore waterfront. The azimuth of this line as it crosses over NYC is 52°, which is also the angle of the sides of the Great Pyramid. The image below is an equal azimuthal projection, also centered on New York City, with this same alignment extended in both directions.

Map image - Roger Hedin

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS The alignment crosses between Teotihuacan and Cholula in Mexico and just as this alignment crosses into Mexico from the gulf it crosses over the ancient city of El Tajin and the pyramid of niches. The alignment also crosses over Baalbek, Lebanon and just north of the ancient city of Troy. The alignment also crosses over Stonehenge. The azimuth of the alignment as it crosses over Stonehenge is 72° west of due north and 72° east of due south, which is not the same as the primary alignment of Stonehenge itself. However, the alignment from the center of Stonehenge to the center of the heel stone is 52° east of due north, which is the same as the azimuth of this global alignment as it crosses over New York City and the same as the angle of the Great Pyramid.

JIM ALISON THE PREHISTORIC ALIGNMENT OF WORLD WONDERS Because the equilateral azimuthal projection below is centered on the maximum latitude of the alignment at 53° 33' N, 23° 35' W, the alignment is horizontal on the image. This is the same alignment that is shown on the two maps above. In addition to the cities on the Eastern Seaboard and the ancient sites listed above, this alignment also crosses over a number of other major cities of the modern era, including Mexico City, the national capital of Mexico; Mobile, Alabama; Atlanta, Georgia; London, the national capital of England; Lille, France, Stuttgart and Munich in southern Germany; Zagreb, the national capital of Croatia; Belgrade, the national capital of Serbia; Sofia, the national capital of Bulgaria; Beirut, the national capital of Lebanon; Damascus, the national capital of Syria; and Riyadh, the national capital of Saudi Arabia.

Map image - Roger Hedin

HISTORICAL GEODESY

RANDOM PHOTO

RANDOM OBJECTS

TAGS